电磁力、强力、弱力和引力，是自然界的四种基本相互作用。其中前三者可以纳入到基于规范场的粒子物理标准模型框架中，引力则由爱因斯坦的广义相对论来描述。然而由于引力的不可重整性，物理学家仍然面对如何将这四种力统一起来的难题，这也是理论物理的终极问题之一。

尽管规范场和引力有非常不同的性质，它们之间存在一些深刻的、甚至是很直接的联系。一个著名的联系是“全息对偶”，它表明d维时空的引力理论可以对偶于其时空边界上(d-1)维时空的规范场论。另一个联系是基于散射振幅研究所发现的“平方关系”，即引力振幅可以用规范场振幅的“平方”来描述，比如早期基于弦理论的KLT平方关系[1]，以及近年来基于色动量对偶的BCJ平方关系[2]。

图1：规范场和引力的两种联系：全息对偶和平方关系。

除了散射振幅，场论中的局域算符也是重要物理量。一个自然的问题是，包含算符的物理量的“平方”是否存在？如果存在又有哪些性质呢？中科院理论物理所的杨刚研究员和原研究助理林冠达（北京大学本科毕业，目前为加州伯克利分校在读研究生）在这一问题的研究上取得新进展，首次将平方关系推广到了包含局域算符的物理量——形状因子。

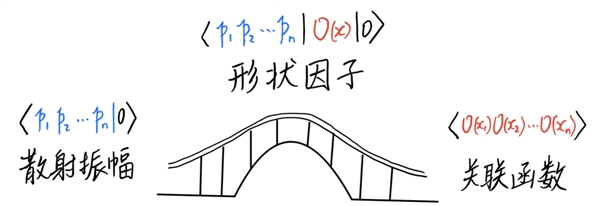
图2：形状因子的特点是既包含渐进物理态又包含局域算符，所以可以作为连接散射振幅和关联函数的桥梁。

这一研究发现了独特的新现象，即规范场理论中的“伪极点”通过平方关系可以转化成引力理论中真实的“物理极点”。场论中物理量的极点有重要的物理意义，比如可以理解为粒子在时空中的传播，即费曼图的传播子。而这里的“伪”极点是指这些极点只是形式上存在，物理量在“伪”极点上并不发散。研究表明，尽管这些“伪”极点隐藏于规范场理论的形状因子中，并不表现出通常极点的发散性质，但通过平方关系这面“照妖镜”，这些极点在引力理论中精确地显示了出来。这一机制有着深刻的物理原因，本质上和引力的万有属性紧密相关。粗略地说，规范场只能和携带色荷的粒子产生直接相互作用，但引力则可以和任意粒子直接耦合，这导致引力形状因子相比于规范形状因子会产生额外的新传播子，也就是新的物理极点。

图3：规范场中的伪极点通过平方关系成为引力理论中的物理极点。

研究进一步发现，即便上面提到的“伪”极点在规范场形状因子中是隐藏的，其特殊性也并非无中生有。具体而言，规范场形状因子在“伪”极点上具有隐藏的因子化性质，而类似的因子化行为通常只在对物理极点处的发散取留数时才会出现。此外，这一研究也首次将平方关系推广到了外线包含色单态粒子的散射振幅，因为规范不变算符可以等效为色单态粒子。这类振幅的一个重要例子就是希格斯粒子和夸克、胶子的散射振幅。感兴趣的读者可以继续参阅关于这一工作的长文章详细介绍[3]。

形状因子的平方关系如何推广到圈图？形状因子在伪极点的隐藏因子化性质如何理解？场论中形状因子的平方关系是否可以推广到弦理论中？这些都是有待进一步研究的问题。这些研究将有助于更好地理解平方关系，从而更好地理解规范场和引力之间的联系和统一。

这一成果近期发表于Physical Review Letters (Vol. 129, 251601, 2022)。该工作得到了国家自然科学基金、中科院先导培育项目等资助。

参考文献

[1] H. Kawai, D. Lewellen, H. Tye, “A Relation Between Tree Amplitudes of Closed and Open Strings”, Nucl.Phys.B 269 (1986) 1-23.

[2] Z. Bern, J. Carrasco, and H. Johansson, “New Relations for Gauge-Theory Amplitudes”, Phys. Rev. D78 (2008) 085011.

[3] G. Lin, G. Yang, “Double copy for tree-level form factors I: foundations”, arXiv: 2211.01386.