|
|
|
|
|
任意磁滞过程的神经网络建模:应用于晶粒取向电工钢 | MDPI Magnetochemistry |
|
|
论文标题:Neural Network Modeling of Arbitrary Hysteresis Processes: Application to GO Ferromagnetic Steel(任意磁滞过程的神经网络建模:应用于晶粒取向电工钢)
期刊:Magnetochemistry
作者:Simone Quondam Antonio, Vincenzo Bonaiuto, Fausto Sargeni and Alessandro Salvini
发表时间:27 January 2022
DOI:10.3390/magnetochemistry8020018
微信链接:
https://mp.weixin.qq.com/s?__biz=MzkyNjI3NjI4Mg==&mid=2247495941&idx=2&sn=
6f3723ba10e1245d5adbb1a269636525&chksm=c23b7ed0f54cf7c620288394bfa907e
a938d187aaa6d2bcc3ad9d1e393d9f244558640432276&token=1916891374&lang=zh_CN#rd
期刊链接:
https://www.mdpi.com/journal/magnetochemistry
引言
本文提出了一个具有高计算效率的磁滞模型,它基于独立的深度神经网络,能够重现任意激励下的磁化演变,并可应用于晶粒取向电工钢的模拟。意大利佩鲁贾大学Simone Quondam Antonio研究团队在Magnetochemistry期刊发表了一篇题为“Neural Network Modeling of Arbitrary Hysteresis Processes: Application to GO Ferromagnetic Steel”的论文。
文中所提出方法的主要创新之处在于将典型的磁滞材料,嵌入到神经网络中,并介绍了一个优化的训练程序。首先,通过Epstein设备对商用晶粒取向电工钢样品进行了实验调查,与国际标准一致;然后,利用传统的Preisach模型,使用三个测量的对称磁滞回线来识别,以产生训练集。一旦网络被训练好,它就会通过再现其他测量的磁滞回线和通过Preisach模拟得到的磁滞过程进行验证。该模型在较低抽象水平上的实现,显示了该模型极高的计算速度和最小的内存分配,具有与有限元分析 (FEA) 耦合的可能。
研究内容
材料:这项工作中研究的铁磁性材料是一种商业晶粒取向铁硅层压合金,等级为M4T27,适用于制造变压器、滤波电感器和创新电动机的性能磁芯。
1. Preisach模型 (PM) 识别
表1中,仅仅是GA就产生了足够准确的参数,成本函数与随后用PSA进行优化后得到的参数非常接近。此外,如果没有初步的全局研究,PSA应该从许多不同的初始点开始启动,分布在空间参数上,使得识别工作变得繁琐,在某些情况下甚至不准确。一旦PM被成功识别,就产生了基于NN的模型用于训练数据集。它由一个主要的磁滞回线组成,有3080个磁场和磁感应序列样本。

表1. 通过遗传算法 (GA) 和模式搜索算法 (PSA) 优化后获得的成本函数的Preisach参数和值。
2. 神经网络训练
图1显示了由六个训练后的神经网络对训练集进行的闭合回线模拟。可以注意到,每层有6个和8个神经元的网络时训练不足。如果每层的神经元数量增加到12个,则会有更高的准确性。然而,如果网络更大,就会达到训练的极限,这点可以从图1f看出。

图1. 六个训练过的网络进行的训练集的回线计算。每个隐藏层的神经元数量等于6 (a)、8 (b)、10 (c)、12 (d)、14 (e)和16 (f)。
3. 对称性回线的模拟
图2显示了Hmax=17A/m到Hmax=140A/m的实验磁滞回线和由PM或基于NN的模型模拟的磁滞回线之间的比较。可以看到,如果磁场小于30A/m时,B的最大值与测量值有轻微偏差。从图2c,d中可以看出,这种偏差在更高的H值中没有出现。

图2. Hmax=17 A/m (a),26 A/m (b),45 A/m (c),140 A/m (d) 的对称磁滞回线 (黑色虚线),与Preisach模型 (蓝色连续线) 和神经网络模型 (红点) 计算的磁滞回线对比。
4. 一阶反转曲线 (FORC) 的模拟
Preisach模型和神经网络模型得到的回线形状之间有很好的一致性,证实了NN在更通用的磁滞模式下有更好的复制Preisach模拟的能力,与训练中应用的磁滞模拟完全不同。图3a,b所示的差异,与Hmin>10A/m的不对称回线有关,几乎可以忽略不计。
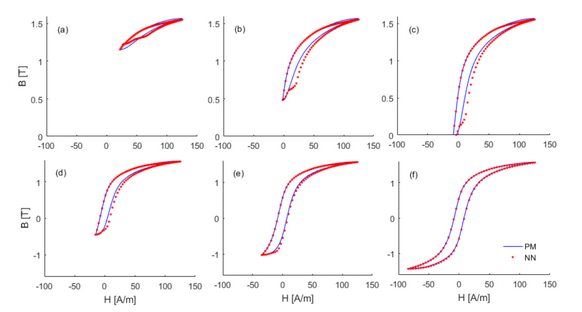
图3. Bmin=1.20T (a)、0.5T (b)、0T (c)、-0.5T (d)、-1.0T (e)、-1.20T (f) 时,Preisach模型 (蓝色连续线) 和神经网络 (红点) 一阶反转曲线模拟的比较。
5. 双音激励波形
相位角影响了子回线的位置,在所有情况下,神经网络都能正确预测。图4中可以看出,由神经网络计算的子回线的位置和形状都与PM模拟结果一致。

图4. 在双声道磁场波形,恒定调制指数m=0.24,以及不同相位角φ=0° (a)、60° (b)、120° (c)、180° (d) 的条件下,由Preisach模型和神经网络计算的磁滞回线的比较。
结论
通过实验或Preisach模型生成的宽激发范围 (高达1.6 T) 再现磁化过程来验证磁滞模型,同时考虑了各种类型的激励波形。通过比较分析突出了神经网络模型具有预测材料磁化演变和能量损失的能力,并且在所有示例中具有较高的准确性。计算和存储效率以及容易反转的可能性,使该模型适合与有限元方案耦合。
Magnetochemistry期刊介绍
主编:Carlos J. Gómez García, Universidad de Valencia, Spain
期刊主要覆盖磁性的所有领域,特别关注磁性材料的设计、合成、表征及其结构和性质关系的研究。
2020 Impact Factor:2.193
5-Year Impact Factor:2.313
Time to First Decision:15.6 Days
Time to Publication:38 Days


特别声明:本文转载仅仅是出于传播信息的需要,并不意味着代表本网站观点或证实其内容的真实性;如其他媒体、网站或个人从本网站转载使用,须保留本网站注明的“来源”,并自负版权等法律责任;作者如果不希望被转载或者联系转载稿费等事宜,请与我们接洽。